笔者:参宿四星云
如需转载,请告知笔者,并在转载处注明出处。
若公式或图片无法正常显示,请点击下载PDF版本 (16.2 MB, 16 Pages)。
本文考虑的粒子是相对论性的、有加速度的,在闵氏时空中的带电粒子。
本文将从麦克斯韦方程组出发,通过李纳-维谢尔势导出电磁场、坡印廷矢量,由此计算单粒子的远场辐射角分布,并画出若干辐射幅角分布图。
1. 前置知识
1.1 电磁势的达朗贝尔方程
从真空中的麦克斯韦方程组出发,即
再使用以下的变换关系引进矢势 与标势 ,二者可以合称为“电磁势”。
可以将 转换为 。在把麦克斯韦方程组转换为 的形式之前,先容我稍微阐释一下这两个新变量。
从 (2a)(2b) 可以看出, 与 确实是某种“势”,这是因为,若给全空间的 与 都加上一个常数,或是使 ( 加上任意的 ,重新计算出的 与 这两个“物理实在”,是不会发生任何变化的。因此,在经典电磁场理论中,无需关心 与 的绝对大小,只需关心它们的时间变化率、旋度散度梯度等等相对的大小,或者说“势场的局部结构”。若不是为了计算方便,也无需定义 与 的零点。
再结合洛伦茨(Lorenz, not Lorentz)规范
可以将 (1a) 与 (1d) 转换为 的如下形式(具体可以是将 (2a)(2b) 代入 (1a) 再联立 (3) 得到 (4a),将 (2a)(2b) 代入 (1d) 再联立 (3) 得到 (4b)。)
以上两式也被称为经典电动力学的达朗贝尔方程,若 则为简单的波动方程。可以清晰地看到,电磁波(在真空中)传播的速度为
以上的两个达朗贝尔方程,形式几乎相同。只需定义以下的两个四维矢量,便可以将 (4a)(4b) 合二为一。定义
还可以再将 与 合二为一,由此定义达朗贝尔算符:
那么 (4a)(4b) 就转换为以下的简洁形式:
如果直接承认 与 是洛伦兹变换四维矢量(事实上,在广义相对论中也可以这么表示),那么,要研究单粒子运动形成的电磁势,只需把(粒子系的电磁势)加以洛伦兹变换。
1.2 李纳-维谢尔势
只要猜出了一组 与 的解(需要满足以上所有方程),那么它在经典电动力学中就可以直接使用。以下笔者不加证明地摆出一组解
这组解就是李纳-维谢尔势(Liénard-Wiechert potentials),也可以写为四维形式:
这里的 ,它并不代表任何坐标系的时间,而是代表源点的时间为 时,源点的状态产生的效应在 时到达场点(真空中电磁信息以光速 传播)。换句话说,场点在 时刻看到的源点,是源点在先前的 时刻的状态。因此,在计算某个场点在 时刻的电磁势或电磁场时,在对源点产生的效应进行积分时,我们需要使用“源点时间” 。在以下的公式推导中,源点的位置、时间、体积总是带一撇。
2. 点电荷产生的辐射
2.1 计算电磁势
本文仅考虑一个点电荷引起的场。那么由上一节李纳-维谢尔势的公式可以看出, 与点电荷的速度有关(),但与加速度无关。根据 (2a), 才与加速度有关。因此,在导出 的时候,无需考虑粒子的加速度,直接计算粒子在 时的静电势,再加以洛伦兹变换,就可以得到 时刻场点的 。
粒子在 时在场点引起的电势,可以在 时(发出辐射时)的粒子参考系 下,可以用静电势来表示:
其中 是粒子发射辐射时,粒子与场点在 系下的距离,要通过洛伦兹变换,可以得到在观测者系 下的距离 ,二者的关系为
其中 为粒子发射辐射时,源点到场点的矢径,其长度为 。
已知粒子系 相对观察者系 的速度为 ,下面将粒子系下的 洛伦兹变换到观测者系下的 :
2.2 计算电磁场与辐射场的表达式
2.2.1 准备工作
根据 (2a)(2b),要算 ,需要算对 关于 的导数。然而,(13a)(13b) 中的 ,都是 的函数,不能直接对 求导。我们需要先把 三者的微分关系弄清。
稍加整理,得到
直接读出
下式是 (14) 的推导中的一个中间结果:
直接读出
这在稍后的推导中可以用到。
那么,我们终于可以开始导出 与 了。
2.2.2 计算 E
不变不变不变不变
为方便,设 ,那么
接下来,计算
那么,合并 (20)(21),并使用 ,得到
2.2.3 计算 B
不变不变不变不变不变
2.2.4 计算辐射场
下面计算坡印廷矢量(Poynting vector),即电磁场的能流密度矢量。
当我们只考虑远场辐射,可以将 表达式(22)的第二项略去,那么粒子的单位立体角辐射功率为
温馨提示: 是观测者受到辐射所用的时间符号, 是粒子发出辐射所用的时间符号,二者都在观测者参考系下。
2.3 几种特定的单粒子辐射场
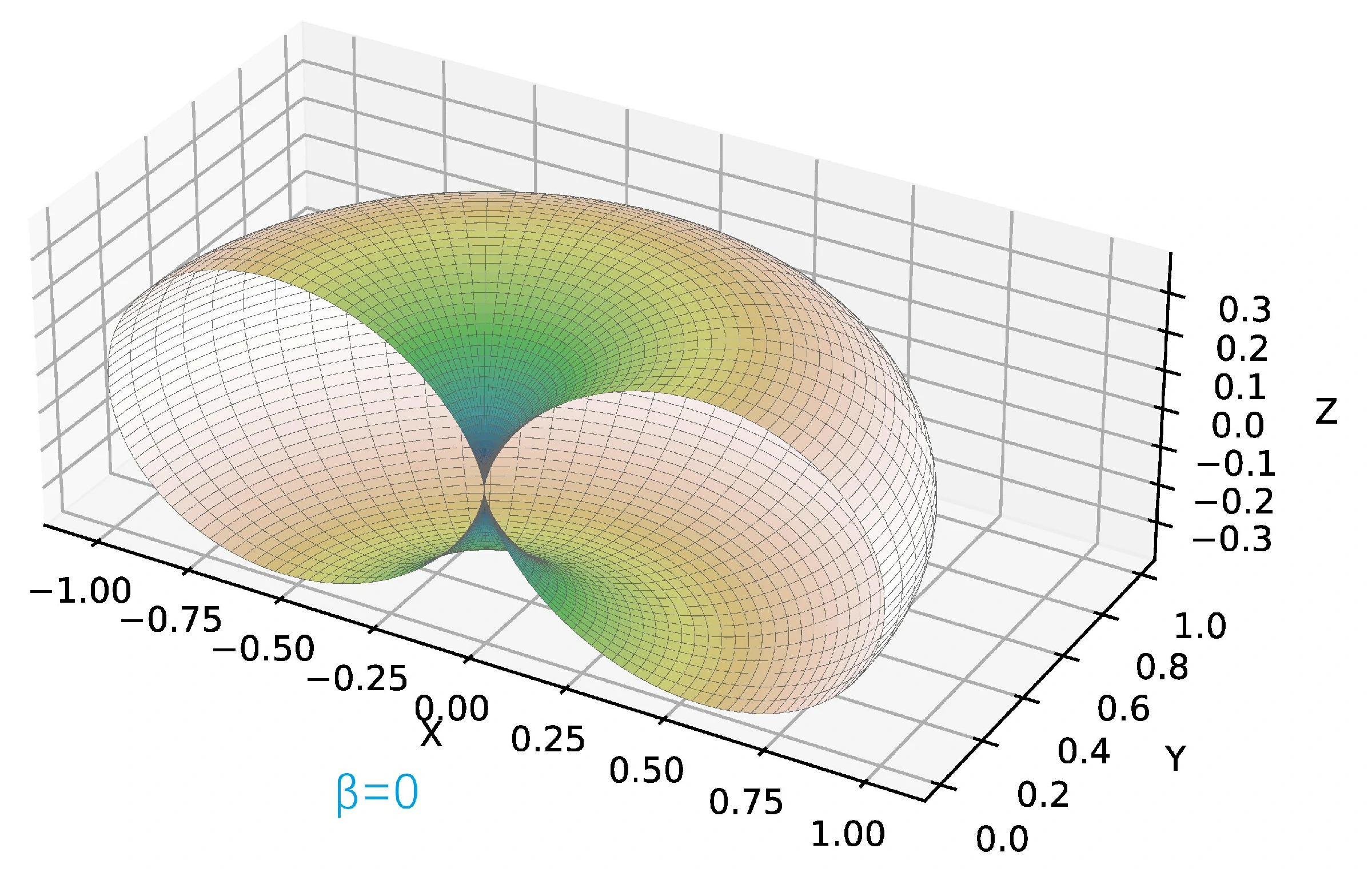
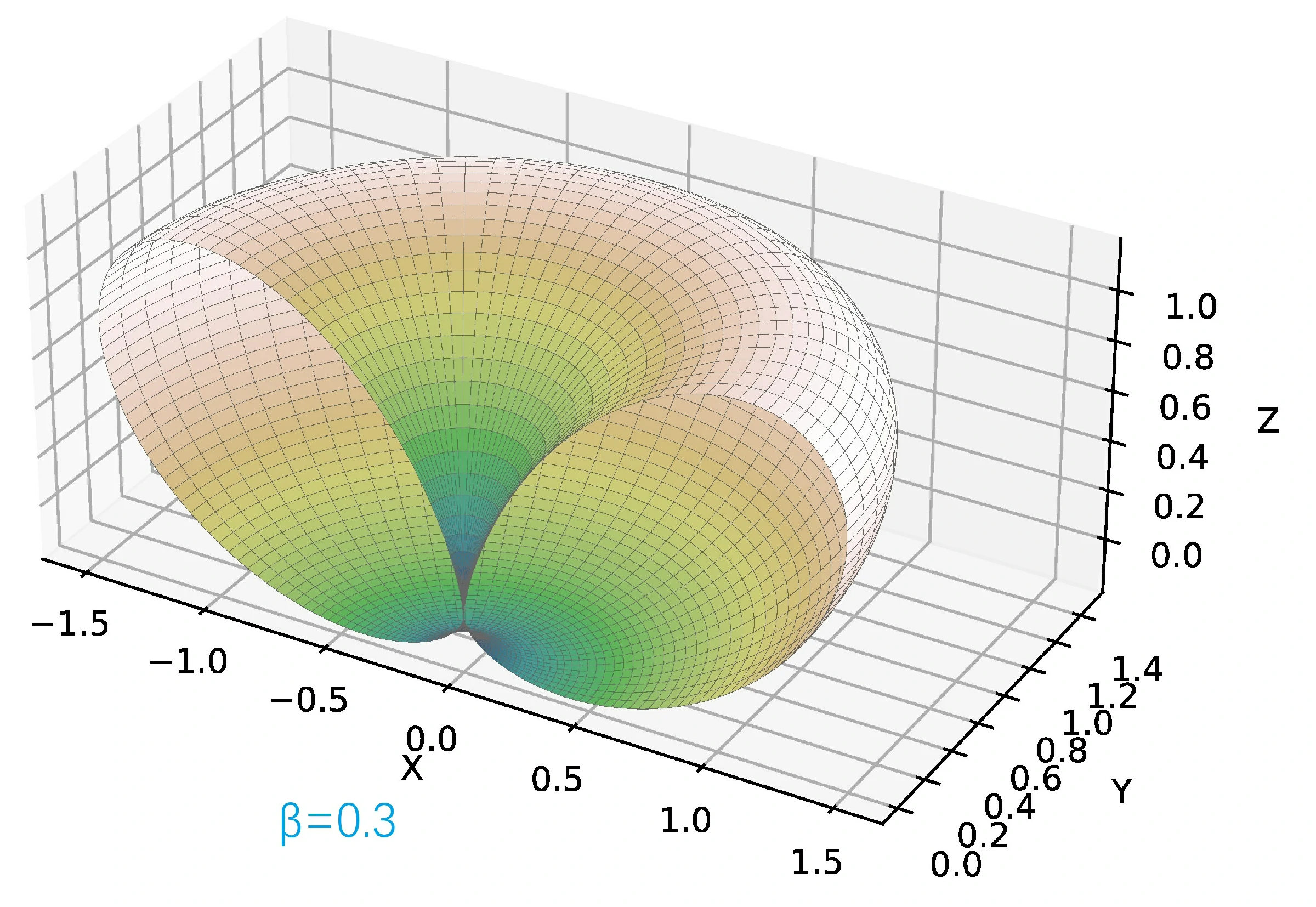
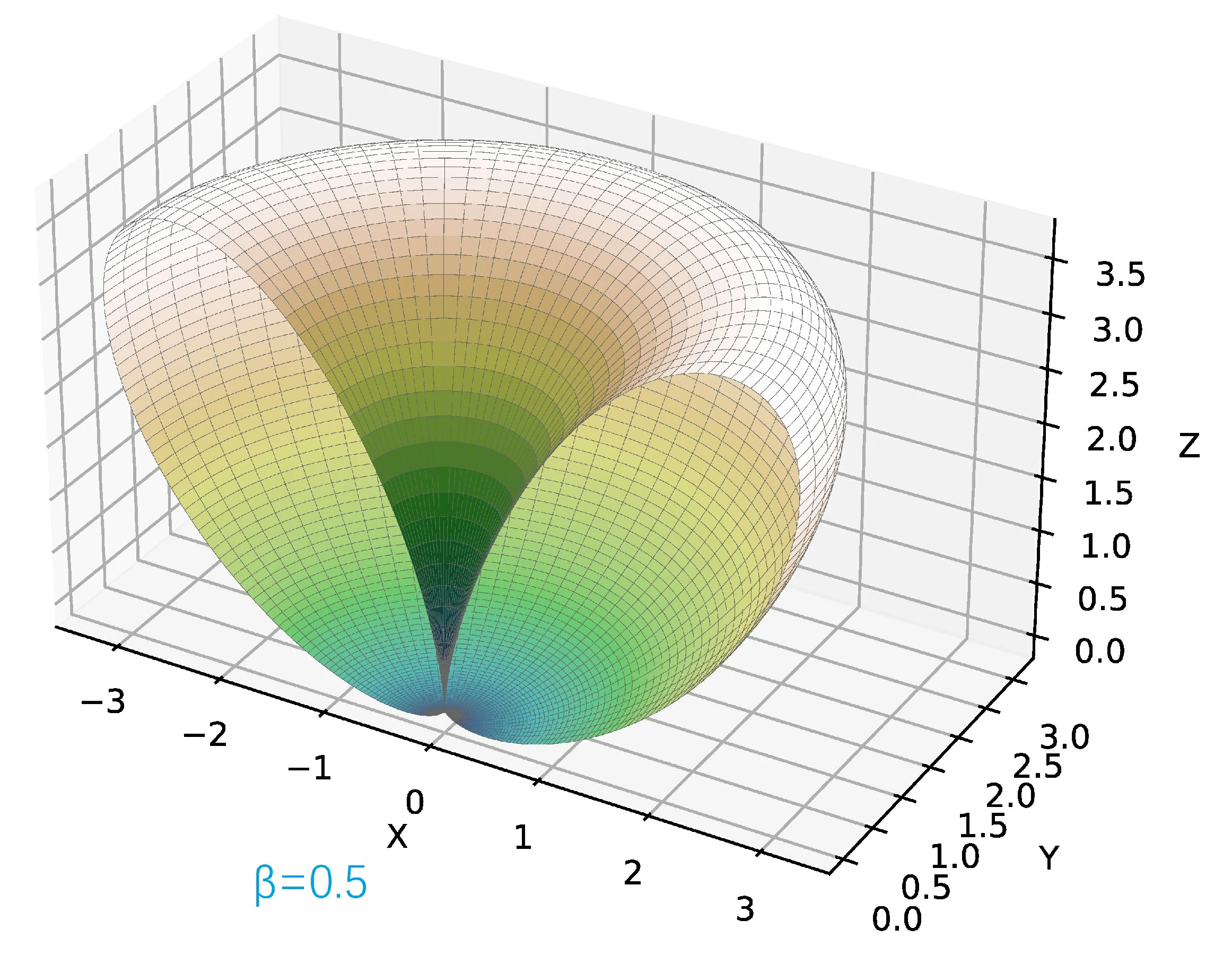
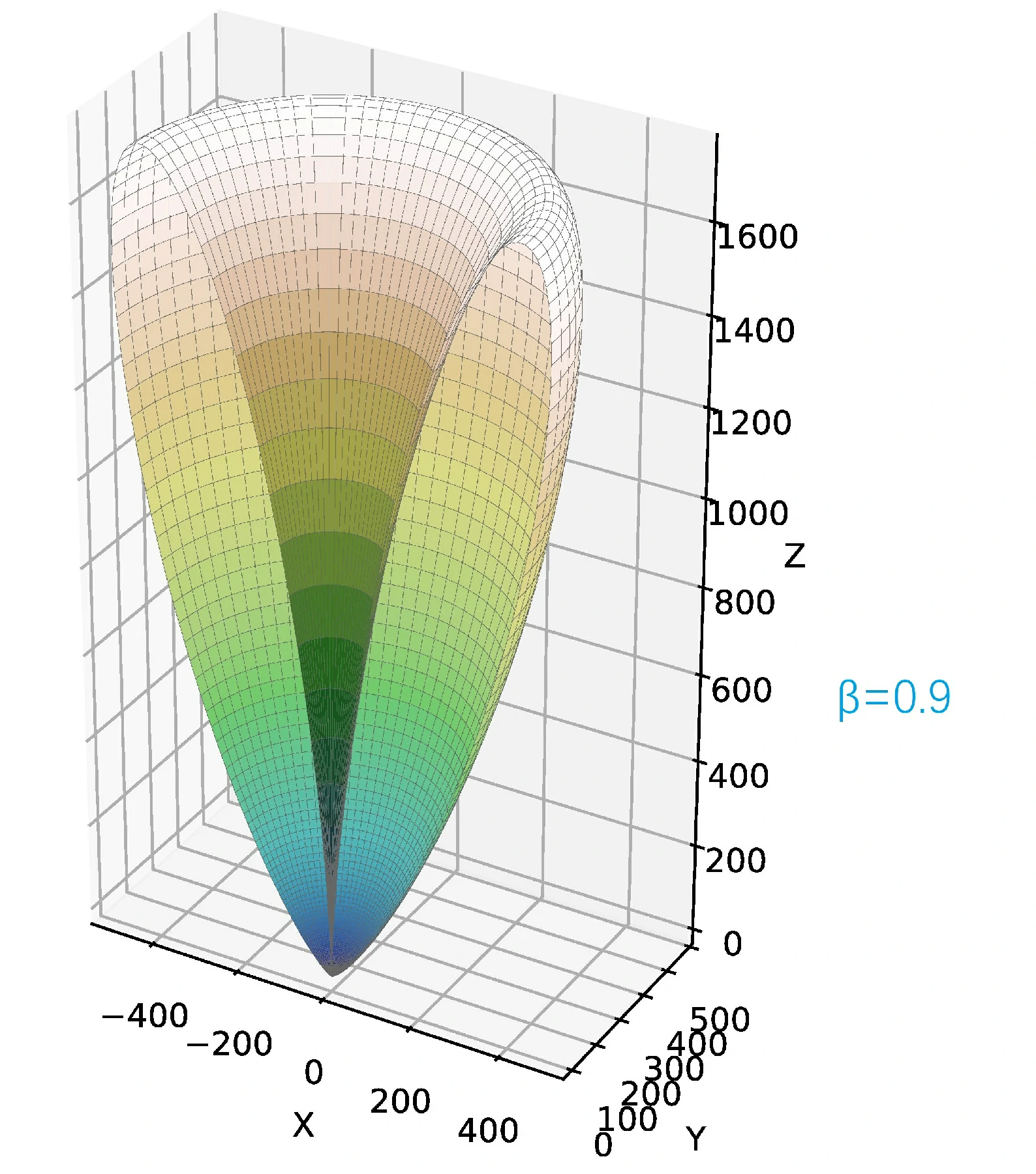
从(25)可以看出,非相对论情况下(),辐射角分布图与速度无关,笔者用 Python 3.12 计算并绘制了非相对论情况下、几种相对论情况下的辐射角分布图。
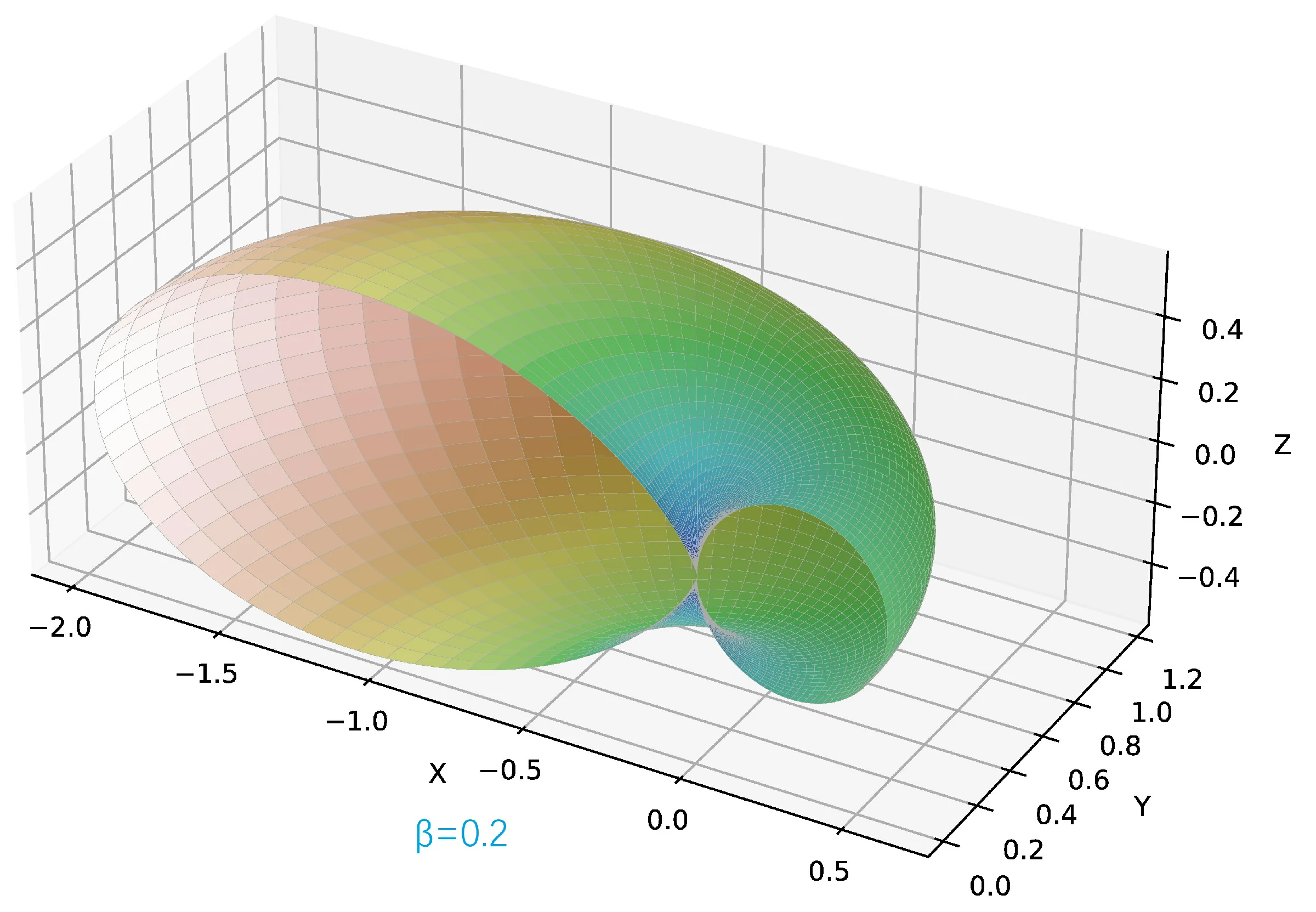
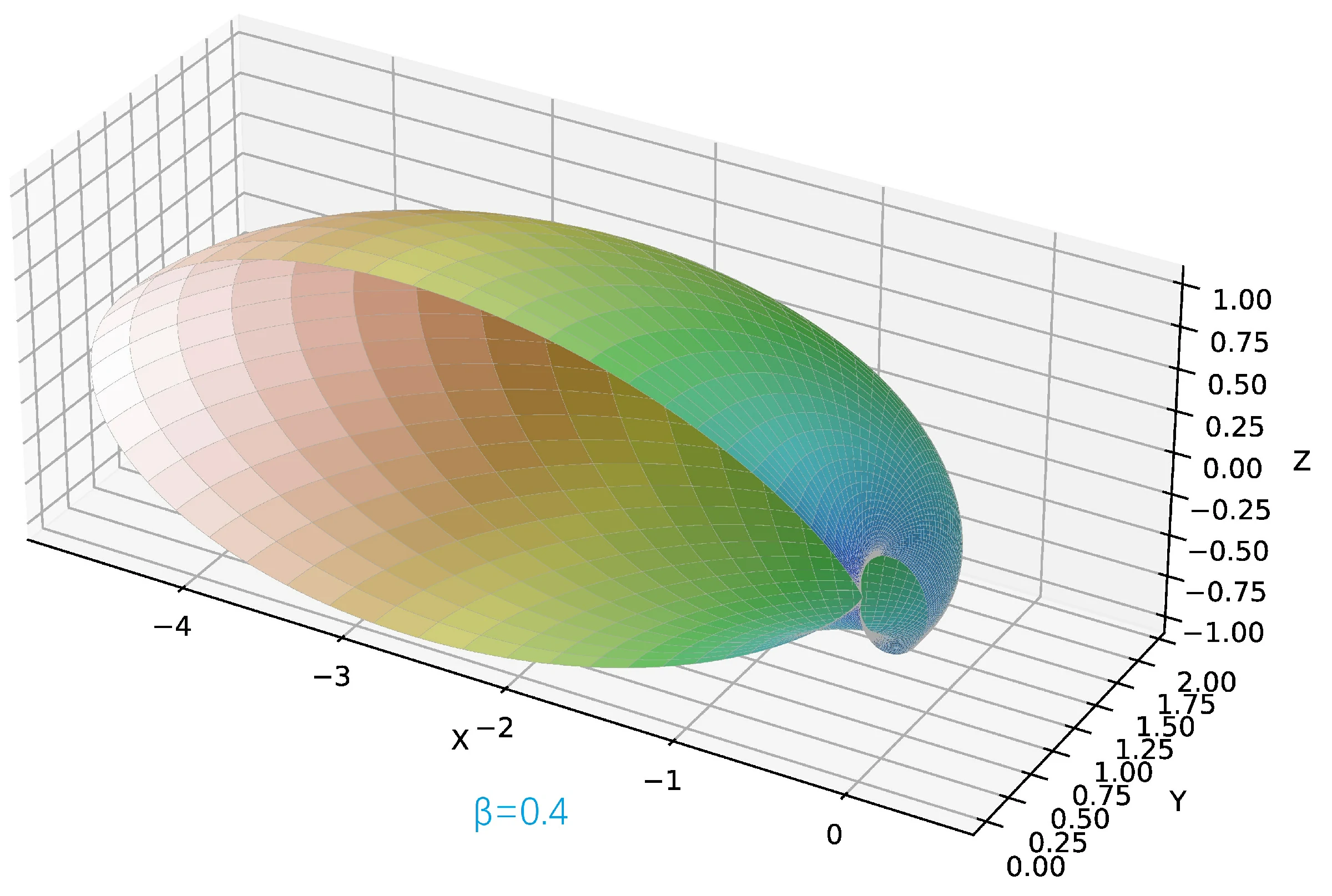
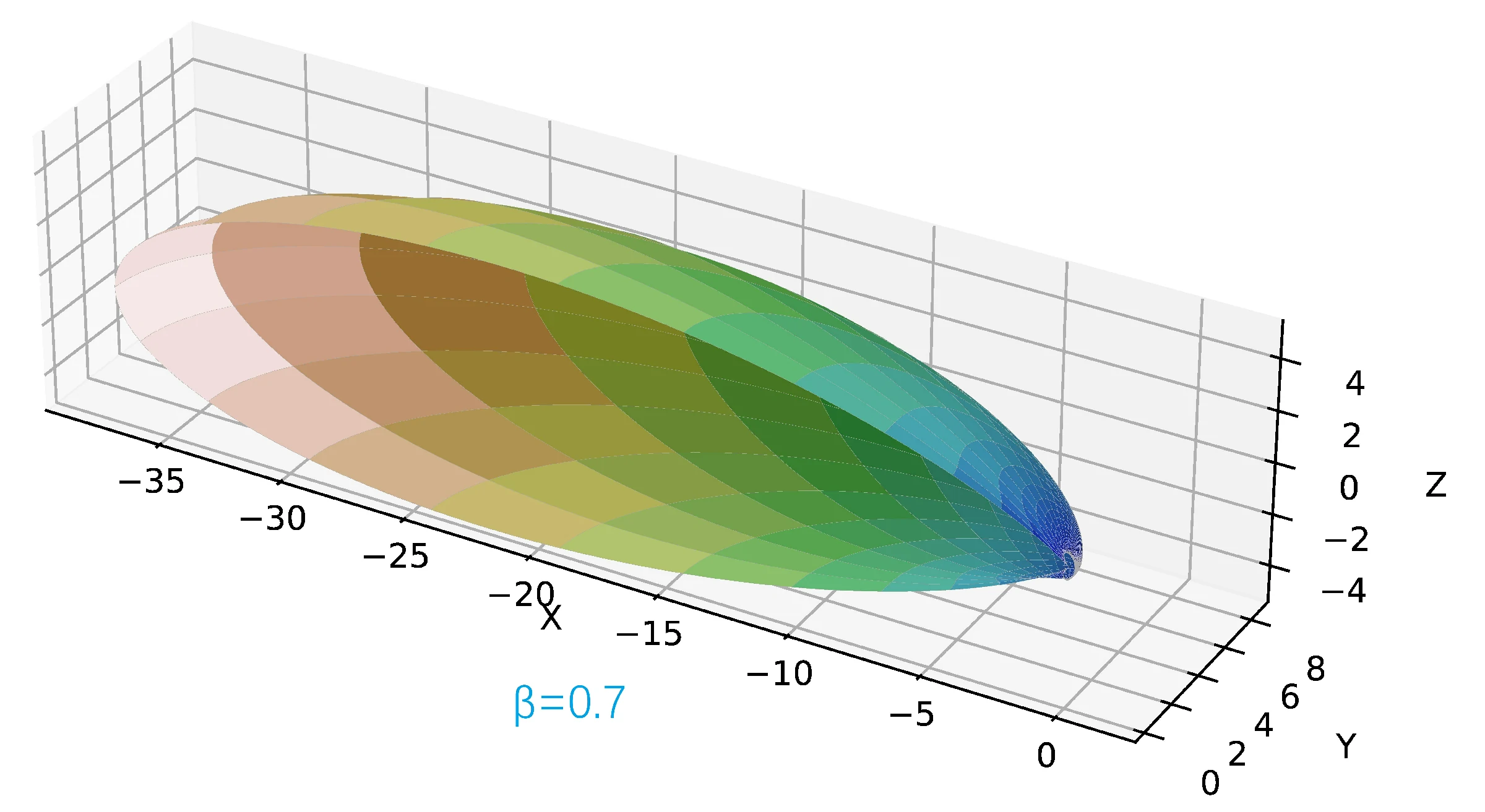
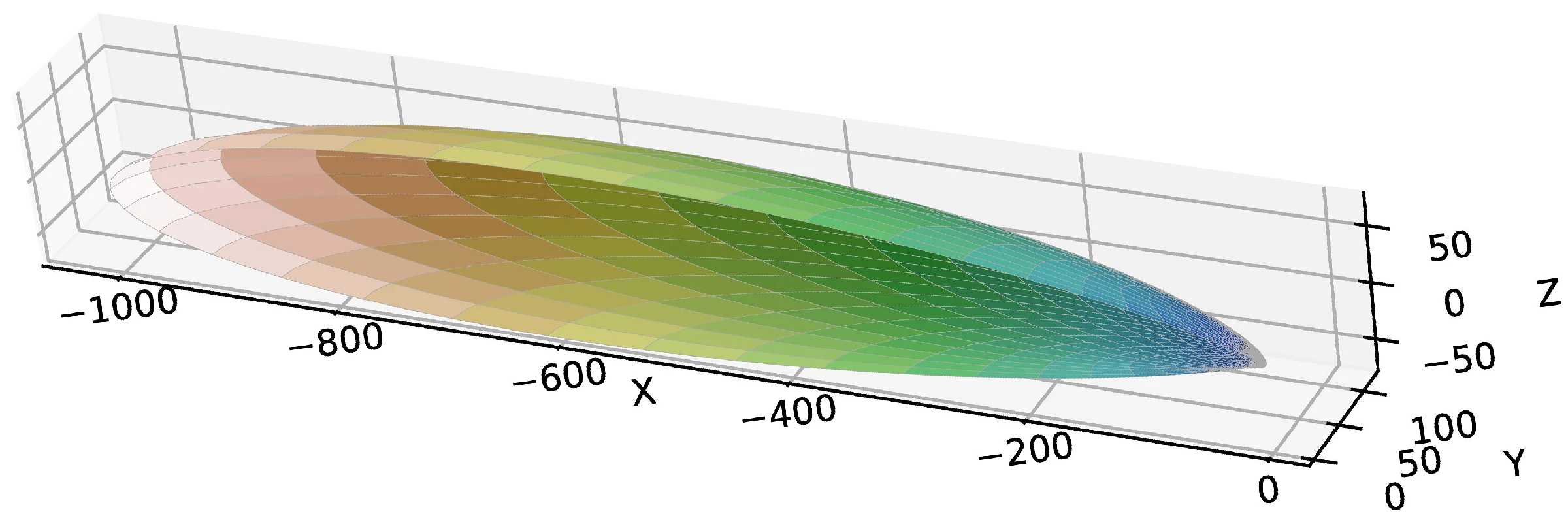
由于以下的角分布图是关于 平面是对称的,为了方便观察,仅画出 的半边。
图中坐标轴的单位是 .
2.3.1 速度为零(或非相对论情况)
加速度沿 轴正方向。

2.3.2 加速度与速度平行
加速度与速度均沿 轴正方向。速度矢量 ,其中 取 的三种情况,依次对应如下的三幅辐射角分布图。



2.3.3 加速度与速度垂直
加速度沿 轴正方向,速度沿 轴负方向。速度矢量 ,其中 取 的五种情况,依次对应如下的五幅辐射角分布图。





2.3.4 一些其他情况



参考文献
[1] 尤峻汉. 天体物理中的辐射机制(第二版)[J], 第七章. 1996.
[2] 郭硕鸿. 电动力学(第三版)[J], 第一章. 2008.
[3] 林伟鹏老师的教导.


.webp)
.webp)
.webp)